Turbo/Centrifugal Supercharger Compressor Sizing
INTRO
There are a couple of good text books available which explain a lot in regards to turbocharger mathematics. These are " Maximum Boost" by Corkey Bell and Turbochargers by Hugh McInnes. Before you really get into turbos too deeply, get these books and read them They are mandatory for better understanding. There are a number of good turbocharger and supercharger web sites as well. Do a Google search and you'll find a lot of them.
Now having said that, I must say that the text and web sites approach the problem far differently than I need. Most grab a turbo and ask "How much horsepower can I make with this turbo? I need to ask, I need this much horsepower, which turbo or supercharger do I need? To that end, I am going to try and demystify the selection process by going through the process of how I selected my twin turbo set up for my Alpine Bonneville time trials car.
WHERE TO START?
In my case, it was with a specific goal! To take a stock "bodied" Sunbeam Alpine and make it go at least 204 miles per hour on the Bonneville Salt Flats. At this speed I hope to have the fastest (maybe not the quickest, though) Sunbeam on the planet!
Well, ok, but how much horsepower will it take to go that 204 mph? First we need the general environmenal conditions at Bonneville during race days in August: temperature is around 95 derees, humidity is around 15 - 30 per cent, barometirc pressure is around 26.5 inches of mercury (note: the barometric pressure reported by the Wendover and Salt Lake City weather stations is a corrected pressure and cannot be used in the equations I use). CAr parameters are: weight about 1800 pounds, drag coefficient is 0.45, frontal area is 17 square feet, mechanical drive line efficiency is 85% (15% losses). I used the Cobra or LSR spread sheet to figure out how much rear wheel horsepower was needed and the math accounts for the mechanical efficiency losses. When I punched these into the spread sheet, I got a rear wheel horsepower requiremen t(RWHP) of 409 hp and a flywheel horsepower (FWHP) of 482 hp.
Because I am a Ford man through and through, I chose to use a 5.0L (302 CID) motor. I had done this some time ago and knew that I was going to need reliability as well as brute force, so I chose a motor made by D.S.S. as their 306. I had this block checked out at the local machine shop in LAs Vegas and it was literally perfect with no bore, measured in four places each, off more than 0.0015 inches. This was a blower block originally and had been used as such. It has 8.5 to 1 pistons and now has a main girdle and windage tray fromm DSS installed. I could have gone the way that many racers go and that is high compression and normally aspirated, but I chose boost.
NOW WE BEGIN IN EARNEST
Fundamental is knowing and understanding volumetric efficiency and an engines ai flow at any desired rpm.
Volumetric efficiency, usually shown as VE, is a measure of how well the engine can gulp air and includes some residual exhaust gasses. There are flow coefficients for all of the different components such as ports, valves, runners, roughness factors, throttle opening, all of which contribute to restriction of air flow into the cylinder. Production cars may have parts which limit the VE to 80% or sometimes less! Most run around 85%, though. Good race parts, such as properly prepared heads and smooth runners may permit numbers in the mid nineties (95%). Once you install a selected set of components, that VE number does not change! Yes, a virtual VE can go higher, but this is with ram tuning to specific power pulses or with power adders. But the real VE does not change until you actually change a hard part. I am using very good heads, AFR 205 cc, which is fully CNC machined multi-angle valve job, and semi polished intake runners on my EFI converted intake manifold. I guess my VE number to be around 93%. I would need a flow bench to test this number, something I do not have (yet).
So....
here is how you determine you engines air flow in cfm. It is significant to note that the air flow in cfm of an engine does not change with any environmental condition, such as going to a higher or lower altitude: mass of flowing air, yes, but not the cfm.
where:
1) the factor of 2 is used because the motor has an intake stroke every other revolution
2) the 1728 converts the cubic inch displacement to cubic feet
3) RPM is the desired motor speed
4) Displacement is motor displacement
In my case, I want to run up against the soft rev limiter built into the EFI computer (but, I can change it if need be), so my operating speed is 6250 RPM and the motor's displacement is 306 cid. Plugging in the numbers.....
Just for laughs, how much horsepower would 515 cfm support? Well, first we need to convert the cfm to lbs of air per minute. That's done simply by multiplying the air flow by the air density. Most turbo shops and tuners use an air density number of 0.69 lbs/ft3. While this is not technically correct for standard temperature and pressure conditions, it is what they test at. So I use it also.
or
Now, we need to convert it to pounds of air per hour by multiplying by 60 min/hr
At an air fuel ratio of 12.5:1 then my fuel needs would be
For normally aspirated motors, it takes 0.5 lbs of fuel per hour to make one horsepower. Then..
And since 341 HP does not equal 482 HP at the flywheel, I need a power adder....
Moving on....
We now have an idea of how to determine operating conditions, so lets detemine how much fuel and air my motor will need to make 482 FWHP. The only new factor needed is that we change from 0.5 lbs of fuel per hr per horse power to 0.55 lbs / hr/ hp. Why? This adds some conservatism to the final air fuel ratio to help with detonation (IMHO).
And the amount of air needed is
This amount of air mass is required no matter where the motor is located, Bonneville or sea level. Boost pressure will change at different environmental conditions, however, to make this number.
And we now have one of the axis numbers on a compressor map! All we have to do now is find the other number, which for a turbo is the pressure ratio,defined as ambient pressure plus boost pressure all divided by ambient pressure. I'll show this below.
Invoking the Equation of State is required. You know that one you all hated in school...
where
P = absolute pressure (lbs/ft2)
V = air flow (cfm)
n = air flow (lbs/min)
R = Universal Gas Constant for air (53.3)
T = Temperature in degrees Rankine (459 + Temp in degrees F)
If we want pressure in PSIA then I need to throw in a factor of 144 in2/ft(sup>2 and then rearrange the terms...
And with numbers..oh, I used 100 degrees for the temperature.
Now this pressure is the ambient pressure plus the boost pressure or
And since the highest altitude I will operate at is at B'ville, the barometric pressure is around 12.8 psia, then the boost pressure can be found!
Thusly
Ok, so the pressure ratio is defined as PR and is Boost + Barometric Pressure, all divided by Barometric Pressure, or
PR = (9.46 + 12.8) / 12.8 = 1.739 = 1.74 approximately.
And we have the other axis value for the compressor map! YeHA!
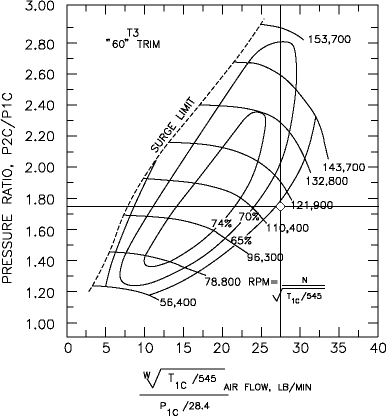
I have marked the pressure ratio, approximately 1.8 and the compressor mass flow rate on the T3 map shown below. The intersection of the lines is where my turbos will operate.

Now, the final thing I need to know is the actual temperature rise due to compressing the air. Why? Well, that temperature and the temperature I assumed are the basis of how much of a temperature drop I need in my intercooler. From the map above, we see that the efficiency at this operating condition is about 65% or so. The equation for compressor outlet temperature is shown below.
Or, putting in the numbers...all in degrees Rankine. Remember here we need the ambient temp at B'ville in August...
So now we have the compressor outlet temperature, the desired charge air temperature for a delta T accross the intercooler. We have the mass flow as well. We have everything known to calculate the intercooler parameters! But, for another chapter...
Everrything above is good for a belt driven compressor exceppt that you ow have to figure in the drive speed. I did not look for a supercharger compressor map, but they are out there and yo can find and use them is pretty much the same way.
so long for now!